TXLS logo

Test Prep

Resource ID: a40R0bzk@8.5
Grade Range: HS - 12
Sections
Test Prep

Test Prep

Multiple Choice

 

9.1 Work, Power, and the Work–Energy Theorem

1.
Which expression represents power?
  1. f d
  2. m g h
  3. m v 2 2
  4. W t
2.

The work–energy theorem states that the change in the kinetic energy of an object is equal to what?

  1. The work done on the object
  2. The force applied to the object
  3. The loss of the object’s potential energy
  4. The object’s total mechanical energy minus its kinetic energy
3.

A runner at the start of a race generates 250 W of power as he accelerates to 5 m/s . If the runner has a mass of 60 kg, how long did it take him to reach that speed?

  1. 0.33 s
  2. 0.83 s
  3. 1.2 s
  4. 3.0 s
4.

A car’s engine generates 100,000 W of power as it exerts a force of 10,000 N. How long does it take the car to travel 100 m?

  1. 0.001 s
  2. 0.01 s
  3. 10 s
  4. 1,000 s

9.2 Mechanical Energy and Conservation of Energy

5.
Why is this expression for kinetic energy incorrect? KE = ( m ) ( v ) 2 .
  1. The constant g is missing.
  2. The term v should not be squared.
  3. The expression should be divided by 2 .
  4. The energy lost to friction has not been subtracted.
6.
What is the kinetic energy of a 10 kg object moving at 2.0 m/s ?
  1. 10 J
  2. 20 J
  3. 40 J
  4. 100 J
7.
Which statement best describes the PE-KE transformations for a javelin, starting from the instant the javelin leaves the thrower's hand until it hits the ground.
  1. Initial PE is transformed to KE until the javelin reaches the high point of its arc. On the way back down, KE is transformed into PE. At every point in the flight, mechanical energy is being transformed into heat energy.
  2. Initial KE is transformed to PE until the javelin reaches the high point of its arc. On the way back down, PE is transformed into KE. At every point in the flight, mechanical energy is being transformed into heat energy.
  3. Initial PE is transformed to KE until the javelin reaches the high point of its arc. On the way back down, there is no transformation of mechanical energy. At every point in the flight, mechanical energy is being transformed into heat energy.
  4. Initial KE is transformed to PE until the javelin reaches the high point of its arc. On the way back down, there is no transformation of mechanical energy. At every point in the flight, mechanical energy is being transformed into heat energy.
8.
At the beginning of a roller coaster ride, the roller coaster car has an initial energy mostly in the form of PE. Which statement explains why the fastest speeds of the car will be at the lowest points in the ride?
  1. At the bottom of the slope kinetic energy is at its maximum value and potential energy is at its minimum value.
  2. At the bottom of the slope potential energy is at its maximum value and kinetic energy is at its minimum value.
  3. At the bottom of the slope both kinetic and potential energy reach their maximum values
  4. At the bottom of the slope both kinetic and potential energy reach their minimum values.

9.3 Simple Machines

9.

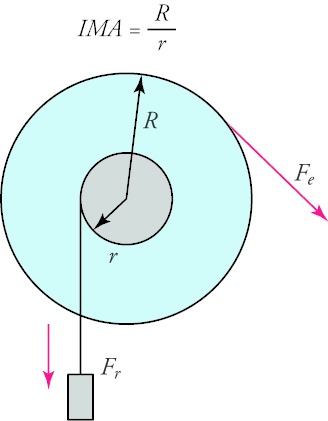
A large radius divided by a small radius is the expression used to calculate the IMA of what?

  1. A screw
  2. A pulley
  3. A wheel and axle
  4. An inclined plane.
10.
What is the IMA of a wedge that is 12 cm long and 3 cm thick?
  1. 2
  2. 3
  3. 4
  4. 9
11. Which statement correctly describes the simple machines, like the crank in the image, that make up an Archimedes screw and the forces it applies?
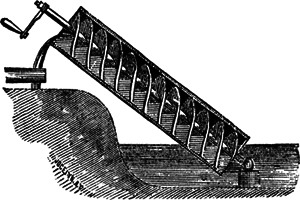
A black and white illustration of Archimedes' screw is shown.
  1. The crank is a wedge in which the IMA is the length of the tube divided by the radius of the tube. The applied force is the effort force and the weight of the water is the resistance force.
  2. The crank is an inclined plane in which the IMA is the length of the tube divided by the radius of the tube. The applied force is the effort force and the weight of the water is the resistance force.
  3. The crank is a wheel and axle. The effort force of the crank becomes the resistance force of the screw.
  4. The crank is a wheel and axle. The resistance force of the crank becomes the effort force of the screw.
12. Refer to the pulley system on right in the image. Assume this pulley system is an ideal machine.
Three pulley systems are shown in side-by-side diagrams. The first consists of a single pulley and is shown holding a mass. The mass is labeled with a force vector, F r, that also points downward. Another force vector, F e, is shown pointing downward from the pulley. N equals one is also shown. The second pulley system consists of a single pulley holding a mass. A force vector, F e, points upward from the pulley. N equals two is shown. The last pulley system shows four pulleys holding a mass with a hook.
Figure 9.16

How hard would you have to pull on the rope to lift a 120 N load?

How many meters of rope would you have to pull out of the system to lift the load 1 m?

  1. 480 N

     
    4 m
  2. 480 N

     
    1 4 1 4 m
  3. 30 N

     
    4 m
  4. 30 N

     
    1 4 1 4 m

Short Answer

 

9.1 Work, Power, and the Work–Energy Theorem

13.
Describe two ways in which doing work on an object can increase its mechanical energy.
  1. Raising an object to a higher elevation does work as it increases its PE; increasing the speed of an object does work as it increases its KE.
  2. Raising an object to a higher elevation does work as it increases its KE; increasing the speed of an object does work as it increases its PE.
  3. Raising an object to a higher elevation does work as it increases its PE; decreasing the speed of an object does work as it increases its KE.
  4. Raising an object to a higher elevation does work as it increases its KE; decreasing the speed of an object does work as it increases its PE.
14.

True or false—While riding a bicycle up a gentle hill, it is fairly easy to increase your potential energy, but to increase your kinetic energy would make you feel exhausted.

  1. True
  2. False
15.

Which statement best explains why running on a track with constant speed at 3 m/s is not work, but climbing a mountain at 1 m/s is work?

  1. At constant speed, change in the kinetic energy is zero but climbing a mountain produces change in the potential energy.
  2. At constant speed, change in the potential energy is zero, but climbing a mountain produces change in the kinetic energy.
  3. At constant speed, change in the kinetic energy is finite, but climbing a mountain produces no change in the potential energy.
  4. At constant speed, change in the potential energy is finite, but climbing a mountain produces no change in the kinetic energy.
16.
You start at the top of a hill on a bicycle and coast to the bottom without applying the brakes. By the time you reach the bottom of the hill, work has been done on you and your bicycle, according to the equation: W = 1 2 m ( v 2 2 − v 1 2 ) If m is the mass of you and your bike, what are v 1 and v 2 ?
  1. v 1 is your speed at the top of the hill, and v 2 is your speed at the bottom.
  2. v 1 is your speed at the bottom of the hill, and v 2 is your speed at the top.
  3. v 1 is your displacement at the top of the hill, and v 2 is your displacement at the bottom.
  4. v 1 is your displacement at the bottom of the hill, and v 2 is your displacement at the top.

9.2 Mechanical Energy and Conservation of Energy

17.

True or false—The formula for gravitational potential energy can be used to explain why joules, J , are equivalent to kg × mg2 / s2 . Show your work.

  1. True
  2. False
18.
Which statement best explains why accelerating a car from 20 mph to 40 mph quadruples its kinetic energy?
  1. Because kinetic energy is directly proportional to the square of the velocity.
  2. Because kinetic energy is inversely proportional to the square of the velocity.
  3. Because kinetic energy is directly proportional to the fourth power of the velocity.
  4. Because kinetic energy is inversely proportional to the fourth power of the velocity.
19.
A coin falling through a vacuum loses no energy to friction, and yet, after it hits the ground, it has lost all its potential and kinetic energy. Which statement best explains why the law of conservation of energy is still valid in this case?
  1. When the coin hits the ground, the ground gains potential energy that quickly changes to thermal energy.
  2. When the coin hits the ground, the ground gains kinetic energy that quickly changes to thermal energy.
  3. When the coin hits the ground, the ground gains thermal energy that quickly changes to kinetic energy.
  4. When the coin hits the ground, the ground gains thermal energy that quickly changes to potential energy.
20.

True or false—A marble rolls down a slope from height h1 and up another slope to height h2, where (h2 h1). The difference mg(h1 – h2) is equal to the heat lost due to the friction.

  1. True
  2. False

9.3 Simple Machines

21. Why would you expect the lever shown in the top image to have a greater efficiency than the inclined plane shown in the bottom image?

The figure shows a nail being pulled out of wood with a crowbar. The image to the right of it shows a representation of all forces and distances in a teeter-totter sketch. A skinny bar represents the crowbar balancing on a triangle, which is where the crowbar rests on the table. The label above it is IMA equals L e over L r. The left side of it is labeled F r, which is where the nail is being pulled out. The front quarter of distance from the end of the crowbar to the pivot of the table is labeled L r. The other three quarters are labeled L e, which is the distance from the pivot to the hand. At the far end is where the hand is pulling on the crowbar and is labeled F e.

The figure shows an inclined plane. The label above it is IMA equals L over h. The first part of the figure shows a long triangle or inclined plane. The back of it is labeled h or the vertical height of the incline, and inside of it is labeled L or the diagonal length of the incline. The incline has a rectangular box on top of it with and arrow pointing it up the incline as an applied force, and it is labeled F e. The second part of it shows a smaller triangle and the back of it is labeled t. The horizontal distance of it is labeled L.

  1. The resistance arm is shorter in case of the inclined plane.
  2. The effort arm is shorter in case of the inclined plane.
  3. The area of contact is greater in case of the inclined plane.
  4. The area of contact is less in case of the inclined plane.
22. Why is the wheel on a wheelbarrow NOT a simple machine in the same sense as the simple machine in the image?
The image shows a two-connected wheel system. It is labeled on top as IMA equals uppercase R over lowercase r. There is a circle with a smaller shaded circle inside. There is an arrow that points from 12 o clock to 7 o clock, and the points of the arrows are labeled uppercase R and lowercase r, which are the outer and inner radius of the two circles. There is an arrow that comes from the top to the right, mounted on the outer wheel, and it is labeled F e. There is a pulley on the bottom with an arrow pointing down beside it, mounted on the inner wheel, and it is labeled F r.
  1. The wheel on the wheelbarrow has no fulcrum.
  2. The center of the axle is not the fulcrum for the wheels of a wheelbarrow.
  3. The wheelbarrow differs in the way in which load is attached to the axle.
  4. The wheelbarrow has less resistance force than a wheel and axle design.
23.

A worker pulls down on one end of the rope of a pulley system with a force of 75 N to raise a hay bale tied to the other end of the rope. If she pulls the rope down 2.0 m and the bale raises 1.0 m, what else would you have to know to calculate the efficiency of the pulley system?

  1. the weight of the worker
  2. the weight of the hay bale
  3. the radius of the pulley
  4. the height of the pulley from ground
24.

True or false—A boy pushed a box with a weight of 300 N up a ramp. He said that, because the ramp was 1.0 m high and 3.0 m long, he must have been pushing with force of exactly 100 N.

  1. True
  2. False

Extended Response

 

9.1 Work, Power, and the Work–Energy Theorem

25.

Work can be negative as well as positive because an object or system can do work on its surroundings as well as have work done on it. Which of the following statements describes:


 
a situation in which an object does work on its surroundings by decreasing its velocity and

 
a situation in which an object can do work on its surroundings by decreasing its altitude?
  1. A gasoline engine burns less fuel at a slower speed.

     
    Solar cells capture sunlight to generate electricity.
  2. A hybrid car charges its batteries as it decelerates.

     
    Falling water turns a turbine to generate electricity.
  3. Airplane flaps use air resistance to slow down for landing.

     
    Rising steam turns a turbine to generate electricity.
  4. An electric train requires less electrical energy as it decelerates.

     
    A parachute captures air to slow a skydiver’s fall.
26.

A boy is pulling a girl in a child’s wagon at a constant speed. He begins to pull harder, which increases the speed of the wagon. Which of the following describes two ways you could calculate the change in energy of the wagon and girl if you had all the information you needed?

  1. Calculate work done from the force and the velocity.

     
    Calculate work done from the change in the potential energy of the system.
  2. Calculate work done from the force and the displacement.

     
    Calculate work done from the change in the potential energy of the system.
  3. Calculate work done from the force and the velocity.

     
    Calculate work done from the change in the kinetic energy of the system.
  4. Calculate work done from the force and the displacement.

     
    Calculate work done from the change in the kinetic energy of the system.

9.2 Mechanical Energy and Conservation of Energy

27.

Acceleration due to gravity on the moon is 1.6 m/s2 or about 16% of the value of g on Earth.


 
If an astronaut on the moon threw a moon rock to a height of 7.8 m, what would be its velocity as it struck the moon’s surface?

 
How would the fact that the moon has no atmosphere affect the velocity of the falling moon rock? Explain your answer.
  1. The velocity of the rock as it hits the ground would be 5.0 m/s. Due to the lack of air friction, there would be complete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
  2. The velocity of the rock as it hits the ground would be 5.0 m/s. Due to the lack of air friction, there would be incomplete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
  3. The velocity of the rock as it hits the ground would be 12 m/s. Due to the lack of air friction, there would be complete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
  4. The velocity of the rock as it hits the ground would be 12 m/s. Due to the lack of air friction, there would be incomplete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
28.
A boulder rolls from the top of a mountain, travels across a valley below, and rolls part way up the ridge on the opposite side. Describe all the energy transformations taking place during these events and identify when they happen.
  1. As the boulder rolls down the mountainside, KE is converted to PE. As the boulder rolls up the opposite slope, PE is converted to KE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
  2. As the boulder rolls down the mountainside, KE is converted to PE. As the boulder rolls up the opposite slope, KE is converted to PE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
  3. As the boulder rolls down the mountainside, PE is converted to KE. As the boulder rolls up the opposite slope, PE is converted to KE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
  4. As the boulder rolls down the mountainside, PE is converted to KE. As the boulder rolls up the opposite slope, KE is converted to PE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.

9.3 Simple Machines

29. To dig a hole, one holds the handles together and thrusts the blades of a posthole digger, like the one in the image, into the ground. Next, the handles are pulled apart, which squeezes the dirt between them, making it possible to remove the dirt from the hole. This complex machine is composed of two pairs of two different simple machines.
A post hole digger is shown with yellow and black handles. The digging apparatus is to the right and the post hole digger is closed.
Figure 9.17
 
Identify and describe the parts that are simple machines and explain how you would find the IMA of each type of simple machine.
  1. Each handle and its attached blade is a lever with the fulcrum at the hinge. Each blade is a wedge.

     
    The IMA of a lever would be the length of the handle divided by the length of the blade. The IMA of the wedges would be the length of the blade divided by its width.
  2. Each handle and its attached to blade is a lever with the fulcrum at the end. Each blade is a wedge.

     
    The IMA of a lever would be the length of the handle divided by the length of the blade. The IMA of the wedges would be the length of the blade divided by its width.
  3. Each handle and its attached blade is a lever with the fulcrum at the hinge. Each blade is a wedge.

     
    The IMA of a lever would be the length of the handle multiplied by the length of the blade. The IMA of the wedges would be the length of the blade multiplied by its width.
  4. Each handle and its attached blade is a lever with the fulcrum at the end. Each blade is a wedge.

     
    The IMA of a lever would be the length of the handle multiplied by the length of the blade. The IMA of the wedges would be the length of the blade multiplied by its width.
30.

A wooden crate is pulled up a ramp that is 1.0 m high and 6.0 m long. The crate is attached to a rope that is wound around an axle with a radius of 0.020 m . The axle is turned by a 0.20 m long handle. What is the overall IMA of the complex machine?

  1. 6
  2. 10
  3. 16
  4. 60

 

Related Items

Resources

No Resources

Videos

No videos.

Documents

No Documents.

Links

No Links.